“For millennia, the enigma of the world of Ideas or Forms, which Plato suggested and advocated, has been challenging the most prominent thinkers of the humankind.”
Burgin, Mark. (2018). Ideas of Plato in the Context of Contemporary Science and Mathematics. Athens Journal of Humanities and Arts. 4. 10.30958/ajha.4.3.1.
“The world model provided by the Existential Triad allows us to analyze various processes that go in science. For instance, physicists are trying to create a theory of everything. However, this is impossible because physics studies only physical, i.e., material systems. So, in the best case, physicists will be able to create a theory of everything on the level of physics as the basic scientific reflection of the material world. However, there are higher than physical levels of reality – biological, psychological, and social. Thus, it becomes, for example, questionable that a physical theory can explain all processes and phenomena in society. At the same time, we already know that everything has structure and, as a rule, not a single one. Thus, the general theory of structures is a theory of everything as its studies everything. Now this theory is only at the initial stage of its development and its development requires work of many researchers.”
MLA 8th Edition (Modern Language Assoc.) Burgin, M. S. Structural Reality. Nova Science Publishers, Inc, New York 2011.
Prologue
Over millennia, our view of the world has changed from consisting of a void and a large number of invisible and indivisible particles, which were called atoms (Leucippus of Miletus (ca. 480 – ca. 420 B.C.E.) and Democritus from Abdera (460-370 B.C.E.)) to vacua consisting of strings. While the path has been rocky at times and we still do not know where it leads to, one thing is clear. Human thought continues the search for that unifying theory which is expected to solve the enigma of the world. In the process, we have seen old ideas rejected and reembraced, new ideas scorned and eventually accepted, even if grudgingly. People often, cancelled without mercy and reembraced with regret. Classical computer science falls in the same category as the ideas and forms proposed by Plato, now explained with the theory of structures by Prof. Mark Burgin, or the limitations of Kepler’s deductions from his observations of the planetary trajectories in discovering hidden planets, or the discovery of the boundaries of Newtonian physics as the particle velocities approach the speed of light or the limitations of classical thermodynamics in explaining the phase transitions in matter using statistical mechanics, which addressed the roles of function, structure and fluctuations. The list goes on.
All of these observations have one thing in common. They all point to structures and their dynamics of evolution under the influence of laws of physics as a common denominator. Information is the difference between these structures as they evolve under the influence of interactions among themselves or the interactions with the external world outside of themselves. As Burgin points out:
- Information is a fundamental constituent of the universe on par with matter-energy, the missing link in the explanation of all the phenomena of the world.
- Information Processing requires Physical Structures
- Information to Knowledge is as Energy is to Matter
In this context, we examine the evolution of classical computer science that has made a huge impact in transforming how we live, communicate, collaborate and conduct commerce while at the same time changing the way how we view ourselves and the world we live in. It allowed us to take information processing to new heights and allowed us to unravel the mysteries of the Genome, explain the inconsistencies of various self-consistent logics when they are not moored into external realities and at the same time is causing huge disruptions in our societies with digital divide caused by information processing monopolies.
In this blog, we examine the boundaries of classical computer science as the velocity of information exchange between various entities increases nearing that of the speed of light. The information access and its velocity is creating the haves and have-nots and the haves attempting to control how the have-nots should behave. The outcome of large fluctuations in information access, processing and its use to influence the participants self-interest is analogous to their role in phase transitions in matter or the emergent behavior exhibited in complex adaptive systems. By understanding the limitations of classical computer science, we argue that the fluctuations and their impact can be managed using cognitive overlays just as biological systems do.
In section 2, we describe classical computer science derived from the Turing’s articulation of the Universal Turing Machine and its stored program implementation by John von Neumann. We discuss the Church-Turing Thesis and its limitations as the velocity of information races toward the speed of light among some components of the information processing structures while leaving others out. In Section 3, we discuss the theory of structures, the role of knowledge structures in information processing and the design of autopoietic automata that generalize the Turing Machines to include cognitive overlay for managing fluctuations in the interactions between various components and their environment. In Section 4, we present some observations on the application of the autopoietic automata to design a new class of information processing structures that provide solutions to current issues with state of the art.
What is Classical Computer Science?
Classical computer science, as we practice it today, can be easily said to have its origins emerge from the simple theory of Turing machine (TM) “replacing the man in the process of computing a real number by a machine which is capable of only a finite number of conditions.” Current IT is based on von Neumann’s stored program control implementation of the Turing machine and addresses concurrent and synchronous distributed computations (connected Turing Machines provide sequential computing). As George Dyson so eloquently pointed out “the stored-program, as conceived by Alan Turing and delivered by John von Neumann, broke the distinction between numbers that mean things and numbers that do things. Our universe would never be the same.”

Turing machine has allowed us to create general purpose computers and “use them to deterministically model any physical system, of which they are not themselves a part to an arbitrary degree of accuracy.” While the Turing machine is a mathematical model of computation that defines an abstract machine, which manipulates symbols on a strip of tape according to a table of rules, the stored program implementation of it consists of a central processing unit (CPU), that is used to carry out computations, which reads the input from a memory device, performs the computation defined by an algorithm and writes the output to the memory. Figure 1 shows the stored program implementation of the Turing machine. The algorithm and the data are converted from symbols into sequences of binary digits and are stored in the memory. Each step of the computation involves the CPU reading the instruction from the program, and perform the operation on the input from the memory and write the output in the memory to be read and operated upon by the next instruction. The operation in the form of binary arithmetic depends solely on the input and the operation defined by the algorithm and is completely deterministic. The evolution of the data halts when there are no more operations to be performed. The operation assumes that there are always enough memory and CPU available for performing the operation. John von Neumann’s first implementation used vacuum tubes to perform the binary arithmetic operations and magnetic drum used for memory. Current generation of computers use microprocessor chips and various forms of memory that provide very fast computations. Figure 2 shows John von Neumann with his computer.

Turing computable functions are those that are easily described by a list of formal, mathematical rules or a sequence of event driven actions such as modeling, simulation, business workflows, interaction with devices, etc. It is interesting to note that the Turing computable functions also include algorithms that define neural networks, which are used to model processes that cannot be described themselves as algorithms such as voice recognition, video processing, etc. Sub-symbolic computing (neural network computation) is enabled by algorithms implemented using symbolic computing.
A universal Turing machine is just a Turing machine (UTM) whose algorithm simulates other Turing machines. That is, the input to the UTM is a description of a Turing machine T and an input for T, and the UTM simulates T, on that input. It’s universal in the sense that, for any problem that can be solved by Turing machines, you could either use a Turing machine that directly solves that problem, or you could use a UTM and give it the description of a TM that directly solves the problem. In effect, all modern general purpose computers are universal Turing machines. Thus, all general purpose computers are equivalent to one another: the differences between them can be entirely subsumed in the algorithms as long as the resources that are required to execute them are same. It is interesting to note that Turing machines executing algorithms in parallel, if they do not directly communicate with one another achieve no more than having two which do communicate; and if they communicate, then, in effect, they are just a single device! (Penrose, Roger. The Emperor’s New Mind (Oxford Landmark Science) (p. 63). OUP Oxford. Kindle Edition.)
Church-Turing Thesis and its Boundaries
Turing machine models the behavior of “the man in the process of computing a real number” (quote from Turing’s paper) and the stored program implementation provides a cognitive apparatus to mimic the process with a machine.
All algorithms that are Turing computable fall within the boundaries of Church Turing thesis which states that “a function on the natural numbers is computable by a human being following an algorithm, ignoring resource limitations, if and only if it is computable by a Turing machine.” The resources here are the fuel for computation consisting of the CPU and memory.
According to Jack Copeland and Onan Shagrir, “the Church-Turing thesis (CTT) underlies tantalizing open questions concerning the fundamental place of computing in the physical universe. For example, is every physical system computable? Is the universe essentially computational in nature? What are the implications for computer science of recent speculation about physical uncomputability? Does CTT place a fundamental logical limit on what can be computed, a computational “barrier” that cannot be broken, no matter how far and in what multitude of ways computers develop? Or could new types of hardware, based perhaps on quantum or relativistic phenomena, lead to radically new computing paradigms that do breach the Church-Turing barrier, in which the uncomputable becomes computable, in an upgraded sense of “computable”?
There are at least, three possible arguments pointing to the limitations of CTT:
- Dealing with functions that are not effectively calculable: As Turing showed, there are uncountably many such functions. It is an open question whether a completed neuroscience will need to employ functions that are not effectively calculable. Does human brain in addition to processing calculable functions, utilize other mechanisms to process information involving functions that are not effectively calculable. How do we model them with machines?
- Dealing with concurrent computing processes that model and manage the physical world using various Turing machine implementations that interact with each other and their environment through a multitude of sensors and actuators: Various levels of abstractions in dealing with program and data in the general purpose computer from 1’s and 0’s at the lowest level to symbols, strings, languages and process schema that define structures and operations on them, have allowed us to graduate from mere computing numbers to information transformation, or operations on multimedia, such as text, audio or video data and finally to computers as mediators and facilitators of interactions between autonomous concurrent and distributed computing processes. The evolution of computing structures as complex adaptive systems pose issues dealing with dynamical changes in the organization and composition to accommodate mobility or evolve and be reconfigured to adapt changes in the interactions that are non-deterministic.
- Dealing with large fluctuations in the demand for and the availability of the computing fuel (CPU and memory): CTT inherently ignores resource limitations for executing the algorithms. However, general purpose computers come with finite resources and the fluctuations in the demand for resources when the computations require more memory or computational speed need immediate attention lest the computation halts.
In this section we will examine these boundaries.
Dealing with Functions That are not Effectively Calculable:
“Premise 1 (Thesis H): A human computer satisfies certain constraints.
Premise 2 (Turing’s theorem): The functions computable by a computer satisfying these constraints are Turing-machine computable.
Conclusion (Turing’s thesis): The functions computable by a human computer are Turing-machine computable.”
The question many mathematicians, computer scientists, philosophers and practitioners of cognitive sciences are asking is “Is the human computer capable of only computing functions that are Turing computable or are there other functions that assist in exhibiting higher order cognitive processes such as memory, historical reasoning to assess risk and take actions that optimize the resources (of which a most important resource is time) to achieve a certain goal. While Turing machine models the current state in data structures and operates on them using an algorithm to produce the next state (as shown in figure 1), the output is solely dependent on the input and the history of the state evolution is completely ignored giving rise to a Markovian evolution. On the other hand, human mind is capable of using memory and the historic context to weigh in on the future state giving rise to a non-Markovian evolution , where the conditional probability of a future state depends on not only the present state but also on its prior state history.
As Oran Shagrir points out, “In 1972, Gödel publishes three short remarks on the undecidability results [1972a]. The third is entitled “A philosophical error in Turing’s work.” Gödel declares: Turing in his [1936, section 9] gives an argument which is supposed to show that mental procedures cannot go beyond mechanical procedures. However, this argument is inconclusive. What Turing disregards completely is the fact that mind, in its use, is not static, but constantly developing, i.e., that we understand abstract terms more and more precisely as we go on using them, and that more and more abstract terms enter the sphere of our understanding. There may exist systematic methods of actualizing this development, which could form part of the procedure. Therefore, although at each stage the number and precision of the abstract terms at our disposal may be finite, both (and, therefore, also Turing’s number of distinguishable states of mind) may converge toward infinity in the course of the application of the procedure [p. 306].”
According to Stanislas Dehaene, Turing machine is not a good description of the overall operation of human cognitive processes. In a recent article titled “What is consciousness, and could machines have it?” by Stanislas Dehaene, Hakwan Lau, and Sid Kouider argue that “the organization of the brain into computationally specialized subsystems is efficient, but this architecture also raises a specific computational problem: The organism as a whole cannot stick to a diversity of probabilistic interpretations; it must act and therefore cut through the multiple possibilities and decide in favor of a single course of action. Integrating all of the available evidence to converge toward a single decision is a computational requirement that, we contend, must be faced by any animal or autonomous AI system and corresponds to our first functional definition of consciousness: global availability.” They propose that the computations implemented by current deep-learning networks correspond mostly to nonconscious operations in the human brain. However, much like artificial neural networks took their inspiration from neurobiology, artificial consciousness may progress by investigating the architectures that allow the human brain to generate consciousness, then transferring those insights into computer algorithms.
Recent advances in Functional Magnetic Resonance studies seem to point a way to discern cognitive information processing and develop a model where a series of Turing Machine like computations are performed in converting analog signals of perception to information for a higher layer of conscious reasoning, coordination and action.
The long and short of these studies present a picture of a sequence of algorithmic-like computations at a sub-conscious level augmented by a global conscious layer of neural network based information processing. As Stanislas Dehaene (Stanislas Dehaene (2014) “Consciousness and the Brain: Deciphering How the Brain Codes our Thoughts” Penguin Books, New York. P 162) points out “What is required is an overreaching theoretical framework, a set of bridging laws that thoroughly explain how mental events relate to brain activity patterns. The enigmas that baffle contemporary neuroscientists are not so different from the ones that physicists resolved in the nineteenth and twentieth centuries. How, they wondered, do the macroscopic properties of ordinary matter arise from a mere arrangement of atoms? Whence the solidity of a table, if it consists almost entirely of a void, sparsely populated by a few atoms of carbon, oxygen, and hydrogen? What is a liquid? A solid? A crystal? A gas? A burning flame? How do their shapes and other tangible features arise from a loose cloth of atoms? Answering these questions required an acute dissection of the components of matter, but this bottom-up analysis was not enough; a synthetic mathematical theory was needed.”
Dealing with Dynamics of Interaction Between Computing Elements and their Environment as a Complex Adaptive System (CAS):
Symbolic computing allows us to automate tasks that can be easily described by a list of formal, mathematical rules or a sequence of event-driven actions such as modeling, simulation, business workflows, interaction with devices, etc. The neural network model (also implemented using symbolic computing) allows computers to understand the world in terms of a hierarchy of concepts to perform tasks that are easy to do “intuitively”, but are hard to describe formally or a sequence of event-driven actions such as recognizing spoken words or faces. General purpose computers allow us to abstract 1’s and 0’s that are processed by the computer to lists of symbols, strings, data structures, languages that operate on them and processes that execute the evolution of computations as shown in figure 1.
Networking technologies also implemented using the same computing processes add another dimension to process workflow automation by distributing the computing elements in space and time and let them communicate with each other at various speeds based on the networking technology available. In essence the output of one computer is connected to the input of the other computer to be processed by the local algorithm.
However, connected general purpose computers are synchronized and concurrent. They are equivalent to sequential machines. The limits of Turing machine implementation, to deal with asynchronous concurrent processes that interact with each other indirectly through their interactions with a common environment, fall into the category of complex adaptive systems and exhibit non-deterministic behavior. Computing combined with communication with concurrent and asynchronous processes interacting with common environment and with each other by exchanging messages gives rise to interactive computation which is extensively discussed in the book “Interactive Computing” edited by Dina Goldin, Scott A. Smolka and Peter Wegner.
According to Goldin and Wegner, “Interaction provides an expanded model of computing that extends the class of computable problems from algorithms computable by Turing machines to interactive adaptive behavior of airline reservation systems, or automatic cars. The paradigm shift from algorithms to interaction requires a change in modes of thought from a priori rationalism to empiricist testing that impacts scientific models of physics, mathematics, or computing, political models of human behavior, and religious models of belief.”
In essence, there is a need to go beyond computing and communication to including cognition, consciousness and culture in the new models of Information processing structures.
Dealing with Resource Limitations:
The success of the general purpose computer has enabled current generation mobile, cloud, and high-speed information processing structures whose main criterion for success of their computation is no longer its termination as Turing machines are designed, but its response to changes – its speed, generality and flexibility, adaptability and tolerance to error, faults and damage. Current business services demand non-stop operation and their performance adjusted in real-time to meet rapid fluctuations in service demand or available resources without interrupting service. Church-Turing thesis boundaries are challenged when rapid fluctuations drive the demand for resource readjustment in real-time without interrupting the service transactions in progress. The speed with which the quality of service has to be adjusted to meet the demand is becoming faster than the time it takes to orchestrate the myriad infrastructure components (such as virtual machine (VM) images, network plumbing, application configurations, middleware etc.) distributed across multiple geographies and owned by different providers. It takes time and effort to reconfigure distributed plumbing coordinating with multiple suppliers, which results in increased cost and complexity.

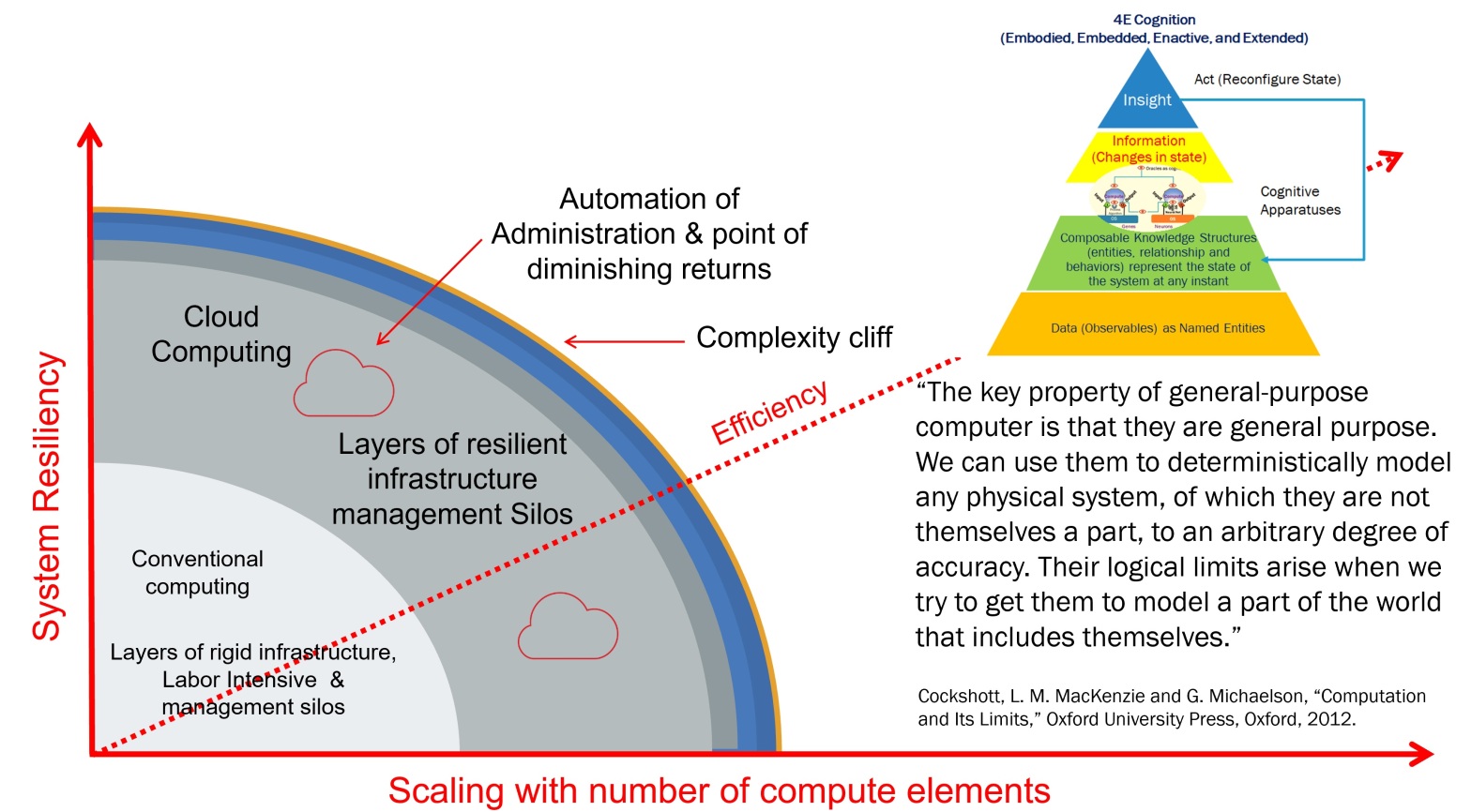
Figure 3 shows the evolution of current computing infrastructure with respect to three parameters—system resiliency, efficiency, and scaling.
The resiliency is measured with respect to a service’s tolerance to faults, fluctuations in contention for resources, performance fluctuations, security threats, and changing business priorities. Efficiency is measured in terms of total cost of ownership and return on investment. Scaling addresses end-to-end resource provisioning and management with respect to increasing number of computing elements required to meet service needs.
As information technologies evolved from server-centric computing to Internet/Intranet-based managed grid and cloud computing technologies, the resiliency, efficiency, and scaling are improved by automating many of the labor-intensive and knowledge-sensitive resource management tasks to meet the changing application/service needs. Current approaches to resource management, albeit with automation, are not sensitive to the distributed nature of transactions, and contention resolution of shared distributed resources, at best, is complex involving many layers of management systems. As von Neumann pointed out (J. V. Neumann, “Theory of natural and artificial automata,” in Papers of John Von Neuman on Computers and Computer Theory, W. Aspray and A. W. Burks, Eds., vol. 12 of Charles Babbage Institute Reprint, Series for the History of Computing, pp. 408–474, The MIT Press, Cambridge, Mass, USA, 1986.), current design philosophy that “errors will become as conspicuous as possible, and intervention and correction follow immediately” does not allow scaling of services management with increasing number of computing elements involved in the transaction. Comparing the computing machines and living organisms, he points out that the computing machines are not as fault tolerant as the living organisms. He goes on to say “it’s very likely that on the basis of philosophy that every error has to be caught, explained, and corrected, a system of the complexity of the living organism would not run for a millisecond.” More recent efforts, in a similar vein, are looking at resiliency borrowing from biological principles and 4E (embodied, embedded, enacted and extended) cognition models to design autopoietic information processing machines.
Epilogue
I am a physicist trained by the Nobel Laureate Prof. Walter Kohn and became a Telecom, Internet and IT practitioner in the Bell system in its heyday. My journey as an accidental computer scientist began in early 2000, when I started to look at the complexity of information technologies and the vision articulated by Paul Horn in 2001, who coined the word autonomic computing to describe a solution to the ever-growing complexity crisis that, still today, threatens to thwart IT’s future growth. “Systems manage themselves according to an administrator’s goals. New components integrate as effortlessly as a new cell establishes itself in the human body. These ideas are not science fiction, but elements of the grand challenge to create self-managing computing systems.” My study led to understanding the problems with distributed computing systems and their management which resulted in a research brief “Designing a new class of distributed systems” in 2011 published by Springer. I published the theoretical and practical implementation findings in the Turing Centenary conference in Manchester (2012), where I had the honor of meeting Roger Penrose and discussing with him the need for a control architecture going beyond Turing computing model. There I also met Peter Wegner again (I had worked with him in adopting object technology to automate business processes at US WEST advanced technologies in the 1980’s) who was also talking about the need for going beyond Church-Turing thesis boundaries. I had the privilege of participating with him in his last conference where he talked about the need for pushing the Church-Turing Thesis boundaries.
In 2013, I discovered Prof. Mark Burgin’s work on super recursive algorithms, named sets, knowledge structures, generalized theory of Turing Oracle, structural machines which offered a unified theory of information processing structures and a path to implementing autopoietic machines.
Autopoietic Machine is a technical system capable of regenerating, reproducing and maintaining itself by production, transformation and destruction of its components and the networks of processes downstream contained in them. It comes closest to realizing the vision of systems managing themselves.
It hopefully makes the statement by Cockshott et al in their book (last paragraph in the last chapter of the book) “Computation and its limits” no longer valid. “The key property of general-purpose computer is that they are general purpose. We can use them to deterministically model any physical system, of which they are not themselves a part, to an arbitrary degree of accuracy. Their logical limits arise when we try to get them to model a part of the world that includes themselves.” Hopefully, this conference on the “Theoretical and Foundational Problems (TFP) in Information Studies” evokes the awareness of key limitations of classical computer science and facilitates a next generation of information processing structures that provide symbiosis between natural and artificial intelligence.